Download the Source Code for this Post
In this post we will use the wave.py module to create audio .wav files that contain tones arranged in the pattern of the iterates of a Cantor set. You can download the final resulting .wav file (372 kB) to hear what it sounds like. The file is series of multiple Cantor arrangements of notes of the chords that make up the chord progression to the beginning of the song “House of the Rising Sun” by The Animals.
A good reference for using wave.py is this stack overflow answer, but this post is designed to be self-contained.
If you want to learn more about the format of .wav files, then this reference from McGill University may be helpful. However, it isn’t really necessary for you to know the details of the .wav file format to use the wave.py module and follow this post.
First, we will review the Cantor set and the iterations that go into its construction. Then we will discuss the code to make the .wav file containing the cantor arrangement of tones.
The Cantor Set
First let’s review how the Cantor set is constructed. First one takes a single interval as pictured in level 0 of the figure below. The Cantor set is made by iteratively deleting intervals of smaller size; the size removed being 1/3 of the current size.
So level 1 is composed of two intervals separated by the middle third of the original interval at level 0. Then level 2 is made from deleting the middle third of each of these two intervals. Again for level 3 we delete the middle third of each interval in level 2.
This process is continued infinitely. Now, you might at first guess that nothing remains if you do an infinite number of such deletions. However, it turns out that there is some set of points that remains, and these points are the Cantor set.
Now, we of course can’t do such an infinite operation on a computer. So we will only be working with an approximation; that is, we will only be looking at a finite number of deletions. In fact we will only work with 5 or 6 levels. In the next section, we will discuss how we will arrange tones to be in the Cantor set pattern.
Arranging Tones in a Cantor Set Pattern
We will actually be using many levels of the construction of the Cantor set. For each level, we will associate one tone from a particular musical chord. The notes will play during the intervals of that level; the deleted parts of that level correspond to the note being held silent.
For example, consider the figure below depicting the arrangment of the five tones of standard C chord on the guitar into a Cantor pattern lasting 3 seconds.
The lower C note will be held for the entire 3 seconds since we attach it to level 0. The lower E note is attached to level 1. It will play for 1 second, rest for one second, and then play again for one second. The G note will play four times for 1/3 seconds each. The higher C (denoted C2) will play 8 times for 1/9 seconds each. The high E (denoted E2) will play 16 times for 1/27 seconds each.
Class to Create Cantor Pattern
First let’s import the modules that we will need:
import wave
import numpy as np
import matplotlib.pyplot as plt
We will make a class for adding sinusoidal tones into a waveform and will add a Cantor pattern of tones into a waveform.
class ToneManipulator:
'''
Class for adding tones to numpy array and converting numpy array to compact data for .wav audio file.
Only deals with single channel .wav files and .wav files that have 2 byte integer values for each frame.
Members
-------
self.framerate : Integer
The number of frames (elements of array) per second.
'''
def __init__(self, framerate):
'''
Initializer
Records the desired framerate. This is used to calculate desired number of frames for a given duration
in seconds.
Parameters
----------
self:
Self-reference to instance.
framerate: Integer.
The number of frames per second for the desired .wav file.
'''
self.framerate = framerate
def createZeroSeries(self, duration):
'''
Create a numpy array of zeroes that represents a given amount of time (in seconds).
Parameters
----------
self :
Self-reference to class instance.
duration : Float
Duration of time in seconds that array represents. This is used to calculate the number
of frames in the array.
'''
nframes = int(self.framerate * duration)
return np.zeros(nframes)
def addWave(self, tSeries, tStart, frequency, amplitude, duration):
'''
Add a wave (giving a certain tone) into a waveform time series. It will only add in the part of the wave
that actually fits into the waveform time series.
Parameters
----------
self :
Self-reference to class instance.
tSeries : Numpy array.
A numpy array for the waveform that the new wave (new tone) will be added to.
tStart : Float
The time that the new wave should start (0.0 is the 0th element of tSeries).
frequency : Float
The frequency of the wave in Hz (periods per second).
amplitude : Float
The amplitude to give the new wave.
duration : Float
How long to make the wave in seconds. This will be converted to the correct number of frames.
If the wave won't fit into the time series, then the part that doesn't fit will be cut off and
not added in.
'''
# If the start of the wave is before 0.0, then cut off the part of the wave that happens
# before 0.0. If there is nothing left of the wave, then just exit.
if tStart < 0.0:
duration += tStart
tStart = 0.0
if duration < 0.0:
return
# Now set up necessary parameters.
angularSpeed = 2.0 * np.pi * frequency / self.framerate
nframes = int(self.framerate * duration)
frameStart = int(self.framerate * tStart)
if frameStart > len(tSeries):
return
endFrame = min(len(tSeries), frameStart + nframes)
wave = amplitude * np.sin(angularSpeed * np.arange(endFrame - frameStart))
tSeries[frameStart:endFrame] += wave
def convertToWaveData(self, tSeries):
'''
Take a numpy array, normalize the values to the 2 byte integer values for .wav file,
and then compactify it into a proper byte array.
Parameters
----------
self :
Self-reference to class instance.
tSeries : Numpy array.
The waveform to create into a data form appropriate to put into .wav file.
'''
# First normalize
seriesMax = np.amax(tSeries)
seriesMin = np.amin(tSeries)
mid = (seriesMax + seriesMin) / 2.0
data = (tSeries - mid) / (seriesMax - seriesMin) * 2.0
# Multiply by max
sampleWidth = 2 # Restrict to using 2 byte integers for .wav file.
maxsize = 2**(8 * sampleWidth - 1) - 1 # Max value for signed integer.
data *= maxsize
# Convert to Integer
data = data.astype(np.int16)
data = data.tobytes()
return data
def _addCantorLevel(self, tSeries, tStarts, duration, levelFreqs, amp):
'''
Private function for doing recursion of adding Cantor levels. Difference between
public function addCantorLevel is that _addCantorLevel uses an array of starting
times.
Members
-------
self :
Self-reference to class instance.
tSeries : Numpy array.
Waveform to add Cantor tones to.
duration : Float
The duration of each interval of this cantor level in seconds.
levelFreqs: Array
The frequencies for this level and the following levels.
amp : Float
The amplitude to use at each level.
'''
# If there are no more frequencies to add, then we stop.
if len(levelFreqs) < 1:
return
# Frequency for this level is just the first frequency in levelFreqs.
freq = levelFreqs[0]
nextStarts = []
nextduration = duration / 3.0
# As we add in waves for each starting point of this level, we also find
# the starting times of the next level.
for start in tStarts:
self.addWave(tSeries, start, freq, amp, duration)
nextStarts.append(start)
nextStarts.append(start + 2 * nextduration)
# Now get the next level; only pass tail of levelFreqs.
self._addCantorLevel(tSeries, nextStarts, nextduration, levelFreqs[1:], amp)
def addCantorTones(self, tSeries, tStart, duration, levelFreqs, amplitude):
'''
Public function to add cantor tones into a waveform. It will only add in the part of the Cantor Tones
that actually fits into the waveform time series.
Members
-------
self :
Self-reference to class instance.
tSeries : Numpy Array.
Waveform that cantor tones are added to.
duration : Float
The length that the cantor tones last overall in seconds. If the duration does not fit into
the time series then the amount that doesn't fit will be cut off.
levelFreqs: Array
An array of frequencies for the tones at each level. The length of the array determines the
number of levels to add.
amplitude : Float
The amplitude to use for all of the tones.
'''
tStarts = np.array([tStart])
self._addCantorLevel(tSeries, tStarts, duration, levelFreqs, amplitude)
Testing Out Tones
First, let’s test out our class’ ability to add tones to a waveform; we will add the tones of the C chord on a guitar in a progressive fashion. The tones will add together to and then take turns fading away to return to the original C note. First, let’s calculate a reasonable frame rate for our .wav file. We will arbitrarily decide that each period of our tones will include at least 10 frames; we don’t include too many to keep the .wav file size small.
# Determine our framerate based on some basic considerations.
minFramesPerPeriod = 10 # We want atleast 10 frames for each period.
maxFreq = 790 # Hz, i.e. periods per second.
framerate = minFramesPerPeriod * maxFreq
print("Using framerate = ", framerate)
We get the following output
Using framerate = 7900
Now let’s write in the notes of the chord and convert the numpy array of our waveform to data usable in a .wav file.
# Parameters for .wav file.
nchannels = 1
sampleWidth = 2
# First we will create a .wav file playing notes in a C chord (as found on a guitar) in progression.
# So we set up variables to hold information for each tone.
# Reference for frequencies of notes are https://www.seventhstring.com/resources/notefrequencies.html
chordFreqs = [261.6, 329.6, 392.0, 523.3, 659.3] # Frequencies of C chord on guitar.
tStarts = [0.0, 0.5, 1.0, 1.5, 2.0]
durations = [4.5, 3.5, 2.5, 1.5, 0.5]
manip = ToneManipulator(framerate)
waveform = manip.createZeroSeries(durations[0])
for freq, tStart, duration in zip(chordFreqs, tStarts, durations):
print("Adding frequency ", freq, " to C chord waveform.")
manip.addWave(waveform, tStart = tStart, frequency = freq, amplitude = 1.0, duration = duration)
data = manip.convertToWaveData(waveform)
Now let’s open a .wav file and write the data to file.
# Open a .wav file and write in the data.
wave_writer = wave.open('2018-01-05-output/cchord.wav', 'w')
wave_writer.setnchannels(nchannels)
wave_writer.setsampwidth(sampleWidth)
wave_writer.setframerate(framerate)
wave_writer.writeframesraw(data)
wave_writer.close()
If you wish, you can download cchord.wav (72kB) to hear what it sounds like.
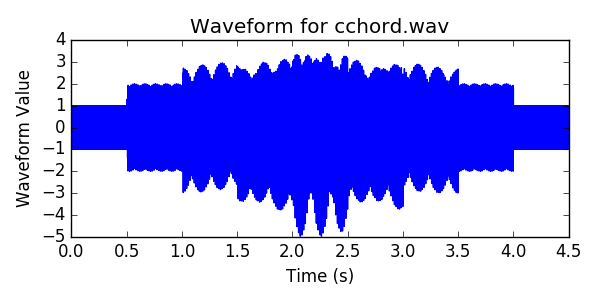
Now, let’s graph the waveform to get an idea of what it looks like.
# Graph what the waveform looks like
times = np.arange(len(waveform)) / framerate
fig = plt.figure(figsize = (6,3))
plt.plot(times, waveform)
plt.title('Waveform for cchord.wav')
plt.ylabel('Waveform Value')
plt.xlabel('Time (s)')
plt.tight_layout()
plt.savefig('2018-01-05-output/cchord.png')
Here is the graph of the waveform for cchord.wav. Note, that we periods of the individual tones are too small to see at the graph’s scale. However, we can see the waves in their amplitudes when they are added together (which if you will recall from trigonometry, is actually at a much lower frequency than the original waves).
Testing a Cantor Progression
Now let’s test our function for adding in a Cantor progression of tones.
# Now let's try set of Cantor tones; the frequency to use at each level will be a frequency
# from the guitar C chord.
duration = 5.0 # Now let the .wav file last 5 seconds.
waveform = manip.createZeroSeries(duration)
manip.addCantorTones(waveform, tStart = 0, duration = duration, levelFreqs = chordFreqs, amplitude = 1.0)
data = manip.convertToWaveData(waveform)
# Write the .wav file.
wave_writer = wave.open('2018-01-05-output/cantor.wav', 'w')
wave_writer.setnchannels(nchannels)
wave_writer.setsampwidth(sampleWidth)
wave_writer.setframerate(framerate)
wave_writer.writeframesraw(data)
wave_writer.close()
You can download cantor.wav (80 kB) to hear the result.
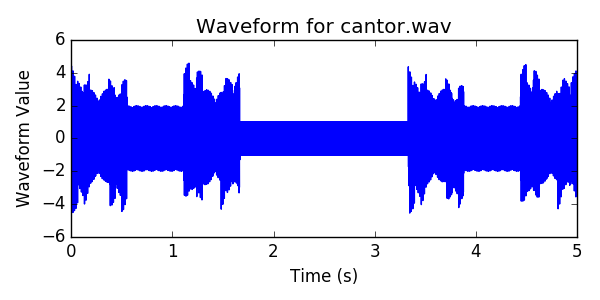
Next, let’s graph the waveform.
# Graph the waveform.
plt.clf()
times = np.arange(len(waveform)) / framerate
plt.plot(times, waveform)
plt.xlabel('Time (s)')
plt.ylabel('Waveform Value')
plt.title('Waveform for cantor.wav')
plt.tight_layout()
plt.savefig('2018-01-05-output/cantorwaveform.png')
Here is a graph of the waveform:
Multiple Cantor Progressions
Now let’s do a chord progression using a Cantor arrangement for each chord. We will use the chord progression for the beginning of the song “House of the Rising Sun” by The Animals. We will use the chord progression found in this guitar tab
# Now let's put in a series of Cantor tones. We will use the chord progression from the beginning of
# the song "House of the Rising Sun" by The Animals as described in the guitar tabs contained at
# https://tabs.ultimate-guitar.com/tab/the_animals/house_of_the_rising_sun_tabs_45131.
duration = 3.0 # Each cantor progression will last 3 seconds.
# Frequencies of notes on guitar for different chords.
chordFreqs = {'Am' : [220.0, 349.2, 440.0, 523.3, 659.3],
'C' : [261.6, 329.6, 392.0, 523.3, 659.3],
'D' : [293.7, 440.0, 587.3, 740.0],
'F' : [349.2, 440.0, 523.3, 698.5],
'E' : [164.8, 246.9, 329.6, 415.3, 493.9, 659.3] }
# The chord progression.
chords = ['Am', 'C', 'D', 'F', 'Am', 'E', 'Am', 'E']
# Open the .wav file to write.
wave_writer = wave.open('2018-01-05-output/cantorProgression.wav', 'w')
wave_writer.setnchannels(nchannels)
wave_writer.setsampwidth(sampleWidth)
wave_writer.setframerate(framerate)
# For each list of chord frequencies in chords, add an arrangement of Cantor tones for the chord.
for chord in chords:
# Re-zero our waveform.
waveform = manip.createZeroSeries(duration)
# We will be adding waveform to the end of the .wav file, so tStart is just 0.0 seconds.
manip.addCantorTones(waveform, tStart = 0.0, duration = duration,
levelFreqs = chordFreqs[chord], amplitude = 1.0)
data = manip.convertToWaveData(waveform)
wave_writer.writeframesraw(data)
wave_writer.close()
You can download cantorProgression.wav (372 kB) to hear the result.